|
BandStrage (CLAPACK) |
帯格納形式
少ないメモリ量で行列[A]を保存し、効率良く計算できるような行列形体する。
＜関数＞
void klku(long int *n, long int *kl, long int *ku, double *a); //従来表示の行列[A]からkl,kuを獲得。
void cs2bs(long int *n, long int *kl, long int *ku, double *a, double *ab); //従来表示の行列[A]を帯格納形式の行列[AB]に格納。
＜引数＞
long int n - (input) 連立一次方程式の式数。正方行列[A]の次数。(n≧0) ここで、行列[A]はn行n列である。
long int kl - (output//input) 行列[A]の帯内の対角下要素の個数。(kl≧0)
long int ku - (output//input) 行列[A]の帯内の対角上要素の個数。(ku≧0)
ku
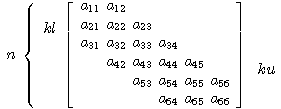
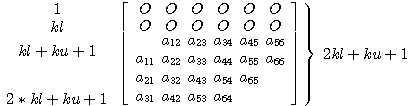
kl n
double a - (input)n行n列の従来の表示形式であらわした行列(但し、行列Aは1次元配列である)。
double ab - (output)n行n列の係数行列[A]を行kl+1から行2*kl+ku+1に対格納形式で入れる。配列の1行〜kl行には値は入れなくても良い。
配列[AB]の第j列には次のように値を格納する(但し行列AおよびABは1次元配列である)。
max( 1, j-ku ) <= i <= min( N, j+kl ) に対して AB( kl+ku+1+i-j, j ) = A( i, j ) を行う。
帯行列状態の行列[A]
a11 a12 * * * *
a21
a22 a23 * * *
a31 a32 a33
a34 * *
* a42 a43 a44 a45
*
* * a53 a54 a55 a56
*
* * a64 a65 a66
行列[A]から作成された帯格納行列[AB]
* * * +
+ +
* *
+ + +
+
* a12 a23 a34
a45 a56
a11 a22 a33 a44 a55 a66
a21
a32 a43 a54 a65 *
a31 a42 a53
a64 * *
|
/* prototype */ void klku(long int *n, long int *kl, long int *ku, double *a); /* function */ void klku(long int *n, long int *kl, long int *ku, double *a) { static long int i,j; static double eps = 1.0E-07; /* initialize */ *kl = 0; *ku = 0; /* j = row , i = col, A[j][i]==a[(j-1)*n+i] */ for( i = 0; i < (*n); i++ ){ for( j = 0; j < (*n); j++){ if( fabs( a[ j * (*n) + i] ) >= eps && ( *ku < j - i )){ *ku = j - i; } } } for( j = 0; j < (*n); j++ ){ for( i = 0; i < (*n); i++){ if( fabs( a[ j * (*n) + i] ) >= eps && ( *kl < i - j )){ *kl = i - j; } } } } |
|
/* define */ #define max(a,b) (a > b) ? a : b #define min(a,b) (a < b) ? a : b /* prototype */ void cs2bs(long int *n, long int *kl, long int *ku, double *a, double *ab); /* function */ void cs2bs(long int *n, long int *kl, long int *ku, double *a, double *ab) { static long int i,j; /* initialize */ for( i = 0; i < (*n) * (2 * (*kl) + (*ku) +1); i++ ){ ab[i]= 0.0; } /* j = row , i = col, A[j][i]==a[(j-1)*n+i] */ /* ab[kl+ku+1+i-j][j]=a[i][j] for max(1,j-ku) <= i <= min(n,j+kl) */ for( j = 1; j <= (*n); j++ ){ for( i = (max( 1, j - (*ku) )); i <= (min( (*n) , j + (*kl) )); i++){ ab[(j-1) * (2*(*kl)+(*ku)+1) + (*kl) + (*ku) + i - j ]= a[ (j-1) * (*n) + i - 1]; } } } |
従来形式の帯行列を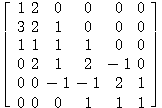
を帯格納形式
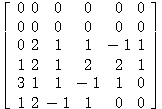に変形する。
|
#include<stdio.h> #include<math.h> #define N 6 int main(void) { static long int i, ldab; static long int n = N; static double A[N*N]; static double *AB; A[0]=1.;A[1]=3.;A[2]=1.;A[3]=0.;A[4]=0.;A[5]=0.; A[6]=2.;A[7]=2.;A[8]=1.;A[9]=2.;A[10]=0.;A[11]=0.; A[12]=0.;A[13]=1.;A[14]=1.;A[15]=1.;A[16]=-1.;A[17]=0.; A[18]=0.;A[19]=0.;A[20]=1.;A[21]=2.;A[22]=-1.;A[23]=1.; A[24]=0.;A[25]=0.;A[26]=0.;A[27]=-1.;A[28]=2.;A[29]=1.; A[30]=0.;A[31]=0.;A[32]=0.;A[33]=0.;A[34]=1.;A[35]=1.; klku(&n, &kl, &ku, A); ldab = 2*kl+ku+1 AB = (double *)malloc(ldab*n*sizeof(double)); cs2bs(&n, &kl, &ku, A, AB); for(i=0;i<36;i++){ printf("%f \t",AB[i]); } printf("%d %d\t",kl,ku); free(AB); return 0; } |
Copyright (C) 2001 Keisuke ABE. All Rights Reserved.