|
DGELQF/ZGELQF (CLAPACK) |
DGELQF/ZGELQF
M行N列の実行列のLQ分解をする。(A=L*Q)
最近風邪気味＆眠いので、近々作ります。ご了承を。まだ、かかります。
＜関数＞
int dgelqf_(integer *m, integer *n, doublereal *a, integer *lda, doublereal *tau,
doublereal *work, integer *lwork, integer *info);
＜引数＞
long int m - (input) 行列[A]の行数。m≧0である。
long int n - (input) 行列[A]の列数。n≧0である。
On exit, the elements on and
below the diagonal of the array contain the m-by-min(m,n)
lower trapezoidal matrix L (L is lower triangular if m <= n);
the elements above the diagonal, with the array TAU, represent
the orthogonal matrix Q as a product of elementary reflectors
(see Further Details).
double a - (input/output) 配列形式はa[lda×n]。
(input) m行n列の行列[A]。
(output) m≧nの時は、DGEQRFによってQR分解された値によって上書きされる。
m<nの時は、DGELQFによってQL分解された値によって上書きされる。
long int lda - (input) 行列Aの第一次元(のメモリ格納数)。lda≧max(1,m) つまり、1〜mの中で一番大きい数よりも、ldaが大きくなければならない。
通常はlda=mで良い。
double tau - (output) 次元数[min(m,n)]の配列。
double work - (workspace/output) 次元数lworkの配列。info = 0のとき、work[0]は最適なlworkが入る。
long int lwork - (input) 配列workの大きさを表す。
lwork≧min(m,n) + max(1,m,n,nrhs)にする。
最適なパフォーマンスを出すためには、lwork≧min(m,n)+max(1,m,n,nrhs)*nbとする。但し、nbは最適なブロックサイズである。
TAU (output) DOUBLE PRECISION array, dimension (min(M,N))
The scalar factors of the elementary reflectors (see Further
Details).
WORK (workspace/output) DOUBLE PRECISION array, dimension (LWORK)
On exit, if INFO = 0, WORK(1) returns the optimal LWORK.
LWORK (input) INTEGER
The dimension of the array WORK. LWORK >= max(1,M). For
optimum performance LWORK >= M*NB, where NB is the optimal
blocksize.
If LWORK = -1, then a workspace query is assumed; the routine
only calculates the optimal size of the WORK array, returns
this value as the first entry of the WORK array, and no error
message related to LWORK is issued by XERBLA.
long int info - (output)
info = 0: 正常終了
info < 0: info = -i ならば、i番目の引数の値が間違えていることを示す。
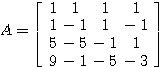をLQ分解する。（解：
、
）
|
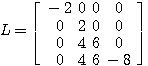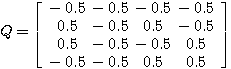#include <stdio.h> #define M 4 #define N 3 double A[M*N]; double b[M*1]; double work[N+M]; int main(void) { long int i; char trans = 'N'; long int m=M,n=N,nrhs=1,lda=M,ldb=M,lwork=M+N,info; A[0]=1.;A[1]=1.;A[2]=1.;A[3]=1.; A[4]=6.;A[5]=-2.;A[6]=-2.;A[7]=6.; A[8]=2.;A[9]=-8.;A[10]=4.;A[11]=14.; b[0]=96.;b[1]=192.;b[2]=192.;b[3]=-96.; ddggeellss_(&trans, &m, &n, &nrhs, A, &lda, b, &ldb, work, &lwork, &info); dgelqf_(integer *m, integer *n, doublereal *a, integer *lda, doublereal *tau, doublereal *work, integer *lwork, integer *info); for(i=0;i<M;++i) printf("%lf\n",b[i]); return 0; } |
Copyright (C) 2001- Keisuke ABE. All Rights Reserved.