Cazoo! Japan CLAPACK DGELS/ZGELS

ホーム > 数値計算ソフトウェア > ライブラリ > LAPACK > CLAPACK > ルーチンの仕様 >

DGELS/ZGELS (CLAPACK)

DGELS/ZGELS

目的

過剰または過小定義の連立一次方程式 [A]{X}={B}の最小2乗または最小ノルム解をQRまたはLQ分解を用いて求める。(行列AはM行N列もしくは、その転置行列)。行列Aをフルランクと仮定している。

いかに示すオプションが提供されている。

1.行列Aは転置無しで、行数の方が大きいまたは等しい場合

最小2乗問題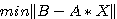を解いて、過剰定義連立方程式の最小2乗解を求める。

2.行列Aは転置無しで、列数の方大きい場合

過少定義式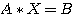の最小ノルム解を求める。

3.行列Aは転置行列で、行数の方が大きいまたは等しい場合

過少定義式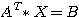の最小ノルム解を求める。

4.行列Aは転置行列で、列数の方が大きい場合

最小2乗問題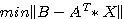を解いて、過剰定義連立方程式の最小2乗解を求める。

仕様

＜関数＞

int dgels_(char *trans, integer *m, integer *n, integer *nrhs, doublereal *a, integer *lda,

doublereal *b, integer *ldb, doublereal *work, integer *lwork, integer *info);

＜引数＞

char trans - (input) 行列Aの転置を含むか含まないのかのフラグ

='N' 行列[A]を含む線形システム。

='V' 行列[A]^Tを含む線形システム。

long int m - (input) 行列[A]の行数。m≧0である。

long int n - (input) 行列[A]の列数。n≧0である。

long int nrhs - (input) 右辺の個数。すなわち(i.e.)、行列BとXの列の数である。nrhs≧0である。

double a - (input/output) 配列形式はa[lda×n]。

(input) m行n列の行列[A]。

(output) m≧nの時は、DGEQRFによってQR分解された値によって上書きされる。

m<nの時は、DGELQFによってQL分解された値によって上書きされる。

long int lda - (input) 行列Aの第一次元(のメモリ格納数)。lda≧max(1,m) つまり、1～mの中で一番大きい数よりも、ldaが大きくなければならない。

通常はlda=mで良い。

double b - (input/output) 配列形式はb[ldb×nrhs]

(input) 右辺ベクトルの行列Bである。行列Bは列ごとにベクトルが格納される。

trans = 'N'ならば、行列Bはm行nrhs列である。

trans = 'T'ならば、行列Bはn行nrhs列である。

(output) 行列Bは列毎に、解ベクトルで上書きされる。

[trans = 'N'でm≧nの場合] 行列Bの1行～n行は最小2乗解ベクトルが入る。

各列における2乗残差は各列におけるn+1要素目～m要素目の2乗残差和で与えられる。

[trans = 'N'でm<nの場合] 行列Bの1行目～n行目（つまり列に）は最小ノルム解ベクトルが入る。

[trans = 'T'でm≧nの場合] 行列Bの1行目～m行目（つまり列に）は最小ノルム解ベクトルが入る。

[trans = 'T'でm<nの場合] 行列Bの1行目～m行目（つまり列に）は最小2乗解ベクトルが入る。

各列における2乗残差は各列におけるm+1要素目～n要素目の2乗残差和で与えられる。

long int ldb - (input) 行列Bの第一次元(のメモリ格納数)。

ldb≧max(1,m,n) つまり、1とmとnの中で一番大きい数よりも、ldbを大きく設定しなければならない。

double work - (workspace/output) 次元数lworkの配列。info = 0のとき、work[0]は最適なlworkが入る。

long int lwork - (input) 配列workの大きさを表す。

lwork≧min(m,n) + max(1,m,n,nrhs)にする。

最適なパフォーマンスを出すためには、lwork≧min(m,n)+max(1,m,n,nrhs)*nbとする。但し、nbは最適なブロックサイズである。

long int info - (output)

info = 0: 正常終了

info < 0: info = -i ならば、i番目の引数の値が間違えていることを示す。

サンプルプログラム

サンプルプログラム(例としては良くない→∵4行3列の行列のくせして、4行ベクトルが右辺ベクトルとなっているので)

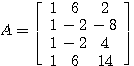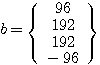、の最小2乗解を求める。（解：）

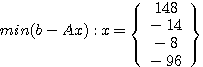#include <stdio.h>

#define M 4

#define N 3

double A[M*N];

double b[M*1];

double work[N+M];

int main(void)

{

long int i;

char trans = 'N';

long int m=M,n=N,nrhs=1,lda=M,ldb=M,lwork=M+N,info;

A[0]=1.;A[1]=1.;A[2]=1.;A[3]=1.;

A[4]=6.;A[5]=-2.;A[6]=-2.;A[7]=6.;

A[8]=2.;A[9]=-8.;A[10]=4.;A[11]=14.;

b[0]=96.;b[1]=192.;b[2]=192.;b[3]=-96.;

dgels_(&trans, &m, &n, &nrhs, A, &lda, b, &ldb, work, &lwork, &info);

for(i=0;i<M;++i) printf("%lf\n",b[i]);

return 0;

}