Cazoo! Japan CLAPACK DGESV/ZGESV

Cazoo! JAPAN

ホーム > 数値計算ソフトウェア > ライブラリ > LAPACK > CLAPACK > ルーチンの仕様 >

DGESV/ZGESV (CLAPACK)

DGESV/ZGESV

目的

一般行列[A]をもつ連立一次方程式 [A]{X}={B} を解く。

仕様

＜関数＞

int dgesv_( integer *n, integer *nrhs, doublereal *a, integer *lda,

integer *ipiv, doublereal *b, integer *ldb, integer *info);

＜引数＞

long int n - (input) 連立一次方程式の式数。正方行列[A]の次数。(n≧0) ここで、行列Aはn行n列である。

long int nrhs - (input) 行列{B}の列数。(nrhs≧0) 通常Bはベクトルなので、通常の使用では1となる。

double a - (input/output) 配列形式はa[lda×n]。

(input)n行n列の係数行列[A]。

(output)LU分解後の行列[L]と行列[U]。ただし、行列[L]の単位対角要素は格納されない。

A=[P]*[L]*[U]であり、[P]は行と列を入れ替える操作に対応し、置換行列と呼ばれ、0か1が格納される。

long int lda - (input) 行列Aの第一次元(のメモリ格納数)。lda≧max(1,n) つまり、1～nの中で一番大きい数よりも、ldaが大きくなければならない。

通常はlda=nで良い。

long int ipiv - (output) 大きさnの配列。置換行列[P]を定義する軸選択用添え字。

double b - (input/output) 配列形式はb[ldb×nrhs]。二次元配列b[ldb][nrhs]の場合は、一次元配列bb[ldb×nrhs]に格納してポインタを渡す。

通常はnrhsが1なので、配列形式がb[ldb]となる。

(input) b[ldb×nrhs]の配列形式をした右辺行列{B}。

(output) info = 0 の場合に、b[ldb×nrhs]形式の解行列{X}。

long int ldb - (input) 配列bの第一次元(のメモリ格納数)。ldb≧max(1,n) つまり、1～nの中で一番大きい数よりも、ldbが大きくなければならない。

通常はldb=nで良い。

long int info - (output)

info = 0: 正常終了

info < 0: info = -i ならば、i番目の引数の値が間違えていることを示す。

0 < info <N-1: 固有ベクトルは計算されていない。

info > N: LAPACK内で問題が生じたことを示す。

サンプルプログラム

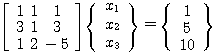を解く。

#include <stdio.h>

#define N 3

double A[N*N];

double x[N];

int main(void)

{

static long int i;

static long int n=N,inc=1,info,piv[N];

A[0]=1.;A[1]=3.;A[2]=1.;

A[3]=1.;A[4]=1.;A[5]=-2.;

A[6]=1.;A[7]=-3.;A[8]=-5.;

x[0]=1.;x[1]=5.;x[2]=10.;

printf("N = %d\n",N);

dgesv_(&n,&inc,A,&n,piv,x,&n,&info);

for(i=0;i<N;++i) printf("%lf\n",x[i]);

return 0;

}

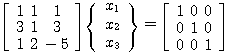を解く。つまり、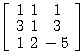の逆行列を求める。

#include <stdio.h>

#define N 3

double A[N*N];

double x[N*N];

int main(void)

{

static long int i;

static long int n=N,inc=3,info,piv[N];

A[0]=1.;A[1]=3.;A[2]=1.;

A[3]=1.;A[4]=1.;A[5]=-2.;

A[6]=1.;A[7]=-3.;A[8]=-5.;

x[0]=1.;x[1]=0.;x[2]=0.;

x[3]=0.;x[4]=1.;x[5]=0.;

x[6]=0.;x[7]=0.;x[8]=1.;

printf("N = %d\n",N);

dgesv_(&n,&inc,A,&n,piv,x,&n,&info);

printf("%lf %lf %lf\n",x[0],x[3],x[6]);

printf("%lf %lf %lf\n",x[1],x[4],x[7]);

printf("%lf %lf %lf\n",x[2],x[5],x[8]);

return 0;

}