Cazoo! Japan CLAPACK DGTSV/ZGTSV

DGTSV/ZGTSV (CLAPACK)

DGTSV/ZGTSV

部分枢軸選択のガウスの消去法によって、連立方程式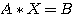を解く。(行列[A]はn行n列の三重対角マトリックス)

ここで、連立方程式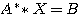を解く場合には、引数duとdlの順序を入れ替えること。

[memo:完全枢軸選択(complete pivoting)法,部分枢軸選択(partial pivoting)法]

＜関数＞

int dgtsv_(integer *n, integer *nrhs, doublereal *dl, doublereal *d__, doublereal *du, doublereal *b, integer *ldb, integer *info);

＜引数＞

long int n - (input) 行列[A]の次数。(n≧0)

long int nrhs - (input) 右辺の個数。すなわち、行列[B]の列数。nrhs≧0。

double dl - (input/output) 次元数[n-1]の配列。

(input) dlには行列[A]の(n-1)個の下対角要素を入れる。

(output) LU分解された行列[A]の上三角行列[U]の(n-2)個の第二上対角要素(dl[0],...,dl[n-3])によって、dlは上書きされる。

double d - (input/outpu) 次元数[n]の配列。

(input) dには行列[A]の対角要素を入れる。

(output) 行列[U]のn個の対角要素によって、dは上書きされる。

double du - (input/output) 次元数[n-1]の配列。

(input) dlには行列[A]の(n-1)個の上対角要素を入れる。

(output) LU分解された行列[A]の上三角行列[U]の(n-1)個の第一上対角要素(dl[0],...,dl[n-2])によって、dlは上書きされる。

double b - (input/output) 次元数[ldb×nrhs]の配列。

(input) n行nrhs列の右辺行列[B]

(output) n行nrhs列の解の行列[X]（ただし、info=0のとき）

long int ldb - (input) 配列Bの第1次元(のメモリ格納数)。ldb≧max(1,n) つまり、1～nの中で一番大きい数よりも、ldbが大きくなければならない。

通常はlab=nで良い。

long int info - (output)

info = 0: 正常終了

info < 0: info = -i ならば、i番目の引数の値が間違えていることを示す。

info > 0: info = i ならば、u[i][i]はゼロとなり解は計算されない。i=nでないならば、LU分解が終わっていない。

[A]{x}={b}を解く、ただし、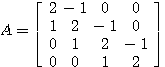,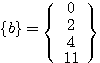。(答え：)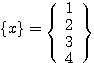

#include <stdio.h>

#define N 4

double DL[N-1],D[N],DU[N-1],B[N];

int main(void)

{

int i;

long int n=N,nrhs=1,ldb=N,info;

DL[0]=1.;DL[1]=1.;DL[2]=1.;

D[0]=2.;D[1]=2.;D[2]=2.;D[3]=2;

DU[0]=-1.;DU[1]=-1.;DU[2]=-1.;

B[0]=0.;B[1]=2.;B[2]=4.;B[3]=11.;

dgtsv_(&n, &nrhs, DL, D, DU, B, &ldb, &info);

for(i=0;i<N;++i) printf("%lf\n",B[i]);

return 0;

}