ホーム > 数値計算ソフトウェア > ライブラリ > LAPACK > CLAPACK > ルーチンの仕様 >

 DGBSV/ZGBSV (CLAPACK)

DGBSV/ZGBSV

一般帯行列[A]をもつ連立一次方程式[A]{X}={B}を解く。

＜関数＞

int dgbsv_(integer *n, integer *kl, integer *ku, integer *nrhs,

              doublereal *ab, integer *ldab, integer *ipiv, doublereal *b,

              integer *ldb, integer *info);

＜引数＞

long int n - (input) 連立一次方程式の式数。正方行列[A]の次数。(n≧0) ここで、行列[A]はn行n列である。

long int kl - (input) 行列[A]の帯内の対角下要素の個数。(kl≧0)

long int ku - (input) 行列[A]の帯内の対角上要素の個数。(ku≧0)

                                   ku
                                      
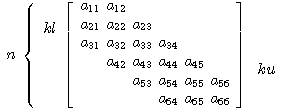
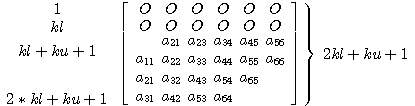
                                                  kl                                                                                    n

long int nrhs - (input) 行列{B}の列数。(nrhs≧0) 通常Bはベクトルなので、通常の使用では1となる。

double ab - (input/output) 配列形式はa[ldab×n]。

               (input)n行n列の係数行列[A]を行kl+1から行2*kl+ku+1に対格納形式で入れる。配列の1行〜kl行には値は入れなくても良い。

               配列[AB]の第j列には次のように値を格納する。

                      max( 1, j-ku ) <= i <= min( N, j+kl ) に対して AB( kl+ku+1+i-j, j ) = A( i, j ) を行う。

               (output)LU分解後の行列[L]と行列[U]の結果。

               ただし、行列[U]は行1〜kl+ku+1にkl+ku個の対角上要素からなる上三角帯行列として格納。

               また、行kl+ku+2から行2*kl+ku+1行にLU分解時に使用した乗数を格納。

long int ldab - (input) 行列ABの第一次元(のメモリ格納数)。(ldab≧2*kl+ku+1)。

            通常はladb=2*kl+ku+1で良い。

long int ipiv - (output) 大きさnの配列。置換行列[P]を定義する軸選択用添え字。

double b - (input/output) 配列形式はb[ldb×nrhs]。二次元配列b[ldb][nrhs]の場合は、一次元配列bb[ldb×nrhs]に格納してポインタを渡す。

               通常はnrhsが1なので、配列形式がb[ldb]となる。

               (input) b[ldb×nrhs]の配列形式をした右辺行列{B}。

               (output) info = 0 の場合に、b[ldb×nrhs]形式の解行列{X}。

long int ldb - (input) 配列bの第一次元。ldb≧max(1,n) つまり、1〜nの中で一番大きい数よりも、ldbが大きくなければならない。

            通常はldb=nで良い。

long int info - (output)

             info = 0: 正常終了

             info < 0: info = -i ならば、i番目の引数の値が間違えていることを示す。

             0 < info <N+1: 固有ベクトルは計算されていない。

             info > N: LAPACK内で問題が生じたことを示す。

 

帯行列状態の行列[A]

a11 a12   *    *    *    *
a21 a22 a23   *    *    *
a31 a32 a33 a34   *    *
 *   a42 a43 a44 a45   *
 *     *  a53 a54 a55 a56
 *     *    *  a64 a65 a66

行列[A]から作成された帯格納行列[AB]

 *     *      *     +     +     +
 *     *      +     +     +     +
 *    a12  a23  a34  a45  a56
a11  a22  a33  a44  a55  a66
a21  a32  a43  a54  a65   *
a31  a42  a53  a64   *     *

計算後の行列[AB]

 *     *      *     u14  u25  u36
 *     *     u13   u24  u35  u46
 *    u12   u23   u34  u45  u56
u11  u22   u33   u44  u55  u66
m21 m32  m43  m54  m65   * 
m31 m42  m53  m64   *      *

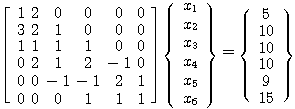を解く。

#include <stdio.h>

#define N 6

double AB[N*N];

double x[N];

int main(void)

{

  static int i;

  static long int n=N,kl=2,ku=1,inc=1,ldab,info,piv[N];

  ldab=2*kl+ku+1;

  AB[0]=0.;AB[1]=0.;AB[2]=0.;AB[3]=1.;AB[4]=3.;AB[5]=1.;

  AB[6]=0.;AB[7]=0.;AB[8]=2.;AB[9]=2.;AB[10]=1.;AB[11]=2.;

  AB[12]=0.;AB[13]=0.;AB[14]=1.;AB[15]=1.;AB[16]=1.;AB[17]=-1.;

  AB[18]=0.;AB[19]=0.;AB[20]=1.;AB[21]=2.;AB[22]=-1.;AB[23]=1.;

  AB[24]=0.;AB[25]=0.;AB[26]=-1.;AB[27]=2.;AB[28]=1.;AB[29]=0.;

  AB[30]=0.;AB[31]=0.;AB[32]=1.;AB[33]=1.;AB[34]=0.;AB[35]=0.;

  x[0]=5.;x[1]=10.;x[2]=10.;x[3]=10.;x[4]=9.;x[5]=15.;

  printf("N = %d\n",N);

  dgbsv_(&n,&kl,&ku,&inc,AB,&ldab,piv,x,&n,&info);

  for(i=0;i<N;++i) printf("%lf\n",x[i]);

  return 0;

}

Copyright (C) 2001 Keisuke ABE. All Rights Reserved.