|
DSYGV/ZHEGV (CLAPACK) |
DSYGV/ZHEGV
実対称/エルミート定値な行列をもつ一般固有値問題の全固有値と、固有ベクトルを計算する。
一般固有値問題の形は、
、 
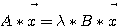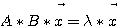、 または 
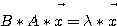
で与えられる。一般固有値は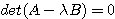
を満たす比の値
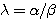である。
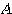と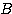
は対称行列であり、
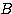は正定値である。
ちなみに、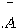
を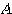
の随伴行列といい、
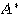で表す。正方行列
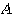が、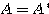
を満たすとき、
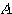をエルミート行列という。特に、実エルミート行列を実対称行列という。
＜関数＞
dsygv_( integer *itype, char *jobz, char *uplo, integer *n, doublereal *a,
integer *lda, doublereal *b, integer *ldb, doublereal *w, doublereal *work,
integer *lwork, integer *info);
＜引数＞
long int itype - (input) 問題のタイプを指定する。規定値は以下の通りである。
= 1: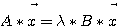 
= 2: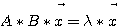 
= 3: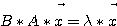 
char jobｚ - (input) 固有値だけを計算するか、固有値と固有ベクトルを計算するかを指定するフラグ。規定値は以下の通りである。
='N' 固有値だけを計算する。
='V' 固有値と固有ベクトルを計算する。
char uplo - (input) 配列AとBに上三角行列を格納するか、下三角行列を格納するかを指定するフラグ。規定値は以下の通りである。
='U' 行列[A]と行列[B]の上三角行列を格納する。
='L' 行列[A]と行列[B]は下三角行列を格納する。
long int n - (input) 正方行列[A]と正方行列[B]の次元数。(n≧0)
double a - (input/output) 配列形式はa[lda×n]。
(input) 対称行列[A]の上三角行列もしくは下三角マトリクスを格納する。
uplo = 'U'のときは、行列Aの上三角部分を、n行n列配列の上三角部分に格納する。
uplo = 'L'のときは、行列Aの下三角部分を、n行n列配列の下三角部分に格納する。
(output)
jobz='V' かつ info = 0 ならば、配列Aには固有ベクトルで構成される行列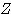
が格納される。
固有ベクトルは次のように正規化される。
itype
= 1 or 2 :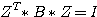 
itype
= 3 :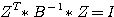 
jobz = 'N' のとき、対角項を含めて上三角部分(←uplo ='U')もしくは、下三角部分(←uplo='L')は破壊される。
long int lda - (input) 行列Aの第一次元(のメモリ格納数)。lda≧max(1,n) つまり、1〜nの中で一番大きい数よりも、ldaが大きくなければならない。
通常はlda=nで良い。
double b - (input/output) 配列形式はb[ldb×n]。
(input) 対称行列[B]の上三角行列もしくは下三角マトリクスを格納する。
uplo = 'U'のときは、行列Bの上三角部分を、n行n列配列の上三角部分に格納する。
uplo = 'L'のときは、行列Bの下三角部分を、n行n列配列の下三角部分に格納する。
(output)
info ≦ N ならば、配列Bには固有ベクトルで構成される行列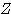
が格納される。
固有ベクトルは次のように正規化される。
itype
= 1 or 2 :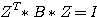 
itype
= 3 :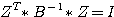 
jobz = 'N' のとき、対角項を含めて上三角部分(←uplo ='U')もしくは、下三角部分(←uplo='L')は破壊される。
long int ldb - (input) 行列Bの第一次元(のメモリ格納数)。ldb≧max(1,n) つまり、1〜nの中で一番大きい数よりも、ldbが大きくなければならない。
通常はldb=nで良い。
double w - (output) 次元数nの配列。info = 0ならば、ｗには固有値が昇順で格納される。
double work - (output) 次元数lworkの配列。info = 0のとき、work[0]は最適なlworkが入る。
long int lwork - (input) 配列workの大きさを表す。
基本的にはlwork≧max(1,3*n-1)で、効率的にするには、lwork≧(nb+2)*nとする。ここで、nbはilaenv_によって返されるdsytrd_のた
めのブロックサイズである。
いずれにしろ、計算性能を向上させるにはlworkを大きくとればよい。といってみるテスト。
long int info - (output)
info = 0: 正常終了
info < 0: info = -i ならば、i番目の引数の値が間違えていることを示す。
info > 0: (DPOTRFもしくはDSYEVが返すエラー番号である）
info <= N: DSYEVが収束しなかった。中間体である三重対角形のi個の非対角要素はゼロに収束しなかった。
info
> N: info=n+i（ただし、1≦i≦n）ならば、Bの主小行列(次数i)は正定値ではない。
Bの分解はできず、固有値・固有ベクトルは計算できなかった。
、
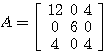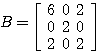の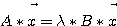
における固有値、固有ベクトルを求める。
|
#include <stdio.h> #define N 3 double A[N*N]; double B[N*N]; double w[N]; double work[3*N]; int main(void) { static long int i; char jobz = 'V'; char uplo ='U'; static long int itype=1,n=N,lda=N,ldb=N,lwork=3*N,info; A[0]=12.;A[1]=999.;A[2]=999.; /* 999が入っている配列の値は利用されない */ A[3]=0.;A[4]=6.;A[5]=999.; A[6]=4.;A[7]=0.;A[8]=4.; B[0]=6.;B[1]=999.;B[2]=999.; B[3]=0.;B[4]=2.;B[5]=999.; B[6]=2.;B[7]=0.;B[8]=2.; dsygv_( &itype, &jobz, &uplo, &n, A, &lda, B, &ldb, w, work, &lwork, &info); for(i=0;i<N;++i) printf("%lf : vector=[ %lf %lf %lf ]\n",w[i] ,A[i*N], A[i*N+1], A[i*N+2]); return 0; } |
Copyright (C) 2001 Keisuke ABE. All Rights Reserved.