Cazoo! Japan SciLab 連立方程式の解法

連立方程式の解法 (SciLab)

連立方程式は、様々な場面で利用されます。特に、最適化問題や逆問題や実験データの曲線近似に対しては、過剰定義式や過少定義式が時として利用されます。Scilabでは、過剰定義および過少定義式でも"\"の記号一つで、最小2乗解を求める事が出来ます。

使用方法

連立方程式が以下で与えられる時に

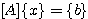
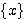は　x=A\b　で解く事が出来ます。(\は英語環境のコンピュータではbackslash)

説明

行列Aが正則行列ならば、x=A\b は x=inv(A)*b と等価である。

行列Aが特異行列ならば、解xは最小二乗解となる。すなわち、norm(A*x-b)が最小となる解となる。行列Aが"Full column rank"、つまり、行列Aのランクが列数と同じならば(大概過剰定義式)、x=A\bはnorm(A*x-b)を最小にする唯一の解である。もし、行列Aが"full coulmn rank"では無いならば、最小二乗解は唯一の解では無い。その場合は大概、x=A\bはノルム最小にする解ではない。この場合の最小ノルム解は、x=pinv(A)*bで与えられる。

A.\B is the matrix with (i,j) entry A(i,j)\B(i,j). If A (or B) is a

scalar A.\B is equivalent to A*ones(B).\B (or A.\(B*ones(A))

A\.B is an operator with no predefined meaning. It may be used to define

a new operator (see overloading) with the same precedence as * or /.

EXAMPLE

A=rand(3,2);b=[1;1;1]; x=A\b; y=pinv(A)*b; x-y

A=rand(2,3);b=[1;1]; x=A\b; y=pinv(A)*b; x-y, A*x-b, A*y-b

A=rand(3,1)*rand(1,2); b=[1;1;1]; x=A\b; y=pinv(A)*b; A*x-b, A*y-b

A=rand(2,1)*rand(1,3); b=[1;1]; x=A\b; y=pinv(A)*b; A*x-b, A*y-b